Towards Zero and Few-shot Knowledge-seeking Turn Detection in Task-orientated Dialogue Systems
무엇에 대한 논문인가
일단 Knowledge-seeking Turn Detection이 무엇인가부터 알 필요가 있다. ai랑 사람이 대화를 하다 보면, 모든 대화에서 retrieval을 해야 하는 것이 아니다. 어떨 때는 그냥 고맙다고 할 수도, 아니면 이미 있는 정보에서 물어볼 수 있는 것이다.
예를 들어 보자. 인공지능에게 감스트에 대해 물어보는 상황이고, 인공지능은 이미 감스트의 나무위키 문서를 모두 알고 있는 상태이다.
1
2
3
4
5
6
7
유저 : 감스트는 뭐하는 사람이야?
인공지능 : 감스트는 인터넷 방송인으로, 주로 게임이나 축구와 관련된 방송을 합니다.
유저 : 그러면 무슨 축구팀을 응원하는데?
인공지능 : 감스트는 EPL의 맨체스터 유나이티드와 한국 국가대표팀을 주로 응원합니다.
유저 : 그렇구만. 뭐 감스트 완전 빡빡이에 모솔처럼 생겼는데. 유튜브 구독자는 엄청 많네 ㄷㄷ
인공지능 : 아닙니다. 감스트는 모태 솔로가 아니며, 유튜버 뚜밥과 결혼을 발표한 상태입니다.
유저 : 뚜밥은 뭐하는 사람인데? 유튜버면 무슨 방송해?
위 대화에서 유저의 1~3번째 질문은 모두 감스트 나무위키에 나와있는 내용들이다. 그런데, 마지막 질문은 감스트가 아닌 뚜밥에 대해서 물어보고 있다. 해당 내용은 나무위키에 나와 있지 않기 때문에, 뚜밥 나무위키에서 뚜밥에 대한 내용을 가져와야 되는 것이다. 바로 1~3번째 질문이 Non-knowledge seeking turn이고, 마지막 질문이 knowledge seeking turn이다. 즉, 검색이 마려운 상황이 knowledge seeking turn이다.
그러면 원래 어떻게 검색이 마려운 상황을 마렵다고 인공지능이 인지하게 했을까? 즉, 어떻게 knowledge seeking turn을 detection했을까?
간단하다. 마려운 상황과 마렵지 않은 상황들의 대화를 다 주고, label을 준다음에, BERT와 같은 모델을 이용해 binary classifier로 훈련시키면 그만이다. 참 쉽죠?
근데, 문제는 위와 같은 대화들과 그것에 대한 label이 다 있어야 한다는 것이다. 이렇게 검색이 마려운지 판단하는 것은 어느 RAG 시스템이든 필요할 것 같은데, 각 분야마다 데이터 만들고 있는 것은 에바 아닌가?
그래서 zero shot 및 few shot으로 knowledge-seeking turn detection을 만들었다는 것이 본 논문의 내용이다. a.k.a 검색 마려운 상황 몇 개만 보고 검색 마려운 상황 감지기 만들기!
그러면 어케했누
이제 논문에서 어떻게 zero-shot 혹은 few-shot 만으로 검색을 할것인지 말것인지 결정했는지 봐보자.
세 가지 단계로 나누어 진다. Encoder Adaptation ⇒ Representation Transformation ⇒ Density estimation
1. Encoder Adaptation
Non-knowledge seeking turn 데이터를 사용해 일반 모델 훈련하듯이 토큰 가려가며 generation 훈련하는 것이다. 그냥 대화 가져다가 파인 튜닝 했다고 생각하면 간단하다. 그게 다임.
2. Representation Transformation
위 모델에서 나온 결과를 간단한 (?) 선형 변환으로 변경해주는 과정이다. 이게 뭔 멍멍이 소리인가 싶겠지만, 대충 나도 비슷하게 생각한다.
대충 본인도 잘 이해 못했기 때문에 설명이 어려울 수 있다. 그리고 잘못된 내용이 있을수도 있다… 본인의 능지 이슈니 착하게 봐주시길 🙏
일단 수식을 보기 전에 알아야 할 것이 있다.
- 이 선형 변환 과정은 knowledge-seeking sentence, 즉 이미 검색이 마려워지는 질문들 몇 개를 가지고 특정 선형 변환을 찾는 것이다.
이제 수식을 보자. \(\tilde{e} = T(e) = (e - \mu)W\)
우리는 $\tilde{e}$를 구해야 한다. 그러면, 여기서 $\mu$가 뭐냐? W는 어떻게 구하느냐? 바로 이렇게다.
\[\mu = \frac{1}{M}\sum^{M}_{i=1}{E(x_i^K)}\]일단, $x_i^K$는 knowledge seeking turn 문장들의 $i$번째 문장이다. 그리고 $E$는 인코더인데, 특정 벡터를 내놓는 모델을 생각하면 편하다. 그러면 $E(x_i^K)$는 그 인코더를 지나서 나온 벡터이다. 그것을 $M$번째 문장까지 더하고 다시 $M$으로 나누어 준 것이니깐, $\mu$는 knowledge seeking turn 문장들의 인코더를 지난 평균 벡터이다.
좋다. $\mu$는 평균벡터이다. 그러면 이제 $W$를 구하기 위해 일단 covariance(공분산) 행렬을 구한다. 이것을 하면 knowledge seeking turn 문장들의 특성들이 나오는 것이다. 이렇게 구한다. \(\sum = \frac{1}{M}\sum^{M}_{i=1}(E(x_i^K) - \mu)^{T}(E(x_i^K) - \mu)\)
그런 다음에, SVD (Singular Value Decomposition)을 수행한다. \(\sum = U\Lambda{U}^T\)
그렇게 $W$를 구할 수 있다..! \(W = U\sqrt{\Lambda^{-1}}\)
마지막으로, $W$의 첫 $L$개의 column을 잘라내서 사용하면 PCA랑 비슷하게 차원은 줄이면서 성능은 유지할 수 있다는데, 저자들의 실험에 따르면 300차원 정도로 해도 95%는 성능이 나왔다고 한다. (근데 이정도 차원 줄이는 것이 큰 의미가 있으려…나?)
자세한 과정은 이 논문에 있다고 한다…
자 그러면 다시 처음 수식을 보자.
\[\tilde{e} = T(e) = (e - \mu)W\]여기서 $e$는 $E(x)$이다. 즉, 문장을 인코더에 넣어서 나온 벡터인데, 이 벡터를 선형 변환 시키는 것이 바로 $T(e)$이고, 그 결과가 $\tilde{e}$이다. 그리고 그 계산 방법이 바로 $(e - \mu)W$, 즉 $(e - \mu)(U\sqrt{\Lambda^{-1}})$이다!
이렇게 몇 개의 문장만으로 $W$랑 $\mu$를 구해 놓을 수 있고, 이렇게 구한 $\tilde{e}$를 사용해서 3단계로 넘어간다.
정리 :
- knowledge-seeking turn에 해당하는 문장 몇 개를 인코더 (모델)에 넣어서 벡터를 구하자.
- 그 벡터들을 사용해서 이렇게 저렇게 하면 선형 변환 벡터가 나온다.
- 그 선형 변환 벡터를 사용하면 이제 다른 문장들도 $\tilde{e}$로 변환할 수 있다. 이것은 PCA랑 이론적으로 같다고 한다.
3. Density Estimation
이제, non-knowledge-seeking turn 문장들을 가져다가, 2단계의 선형 변환을 해서 ${\tilde{e}_1^{NK}, …,\tilde{e}_N^{NK}}$(변형된 문장들)을 얻을 수 있다. 이제 이거를 unit vector로 normalize한다. 그 다음에, Gaussian Mixture Model(GMM) 같은 작은 모델을 훈련한다.
결과적으로, 인코더 E와, 선형변환 T와, 작은 모델 D를 이용해 문장의 점수를 낼 수 있다. \(D(T(E(x)))\)
이게 threshold $\eta$를 넘으면 non-knowledge-seeking turn이라고 판단하면 된다! $\eta$는 training set에서 적당하게 정하면 된다.
이렇게 하면 앞으로의 non-knowledge-seeking turn인 문장들은 높은 값, 아닌 것들은 낮은 값으로 나오게 된다!
얼마나 좋은데?
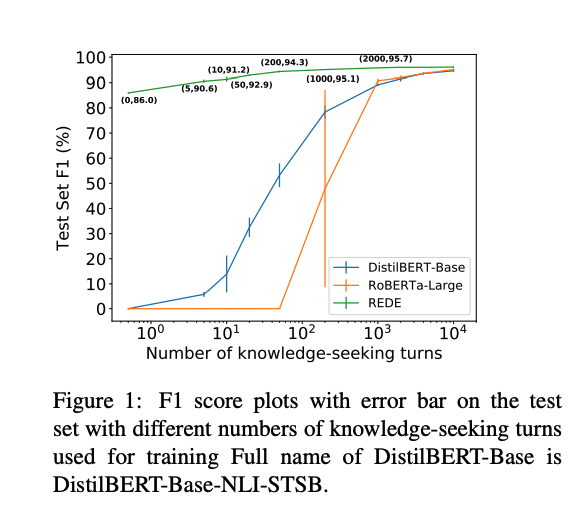
초록색이 위 REDE 기법이고, 주황색과 파랑색은 본래 기법으로 fine-tuning 한 것이다. 그리고 x축은 knowledge-seeking turn 문장들인데, 이것들이 엄청 적을 때에도 REDE는 완전 높은 성능을 내고 있다.
직접 해 보았다~
진짜 잘된다. 이.왜.진? DSTC11-Track5 데이터셋으로 직접 해보았다. 논문에서 나온 DSTC9-Track1의 심화버전?이라고 할 수 있다.
테스트 데이터셋 중 500개를 샘플해서 테스트에 사용했다. non-knowledge-seek turn 데이터 역시 부족한 상황이 있을 것이라고 확신했기에, 이것에 대한 실험도 진행했다.
- validation 데이터로 threshold를 찾았고, 이를 위해 train set의 20% 만큼만 사용했다.
먼저, non-knowledge-seek turn 데이터를 50개로 고정하고 실험해보았다.
| knowledge seek trun 데이터 수 | 2-shot | 3-shot | 5-shot | 10-shot |
|---|---|---|---|---|
| Precision | 0.9141 | 0.8928 | 0.875 | 0.9127 |
| Recall | 0.9459 | 0.9652 | 0.9729 | 0.9691 |
| F1 Score | 0.9297 | 0.9276 | 0.9213 | 0.9401 |
knowledge-seek turn 데이터 수가 10-shot이 가장 좋기는 했는데 2~5shot까지는 별 차이가 나지 않는다. 차이 폭도 크지 않아서, 2개의 데이터만 있어도 엄청 괜찮은 성능을 보여준다.
그리고, knowledge-seek turn 데이터를 10개로 고정하고 실험했다.
| Non-knowledge seek trun 데이터 수 | 5-shot | 10-shot | 50-shot | 100-shot |
|---|---|---|---|---|
| Precision | 0.87188 | 0.89605 | 0.9127 | 0.9471 |
| Recall | 0.94594 | 0.96525 | 0.9691 | 0.9691 |
| F1 Score | 0.90740 | 0.92936 | 0.9401 | 0.95801 |
총 데이터가 15개밖에 되지 않아도 0.9 정도의 F1 Score가 나와준다. 생각보다 성능이 되게 괜찮다! 논문에는 안 나와 있어서 몰랐는데, 이거 두 레이블 모두 많지 않아도 괜찮다. 10개-10개 정도만 만들 수 있으면 쓸만한 성능을 뽑아줄 것 같다.
참고로, 해당 데이터셋으로 supervised learning한 모델들은 0.99는 가볍게 넘는 F1 score를 보여주기는 한다… 그래도, 데이터셋 20개 정도만 구축할 수 있으면 된다는 것이 REDE의 엄청난 메리트 되시겠다~
코드
RAGchain에서 바로 써 볼 수 있다! 코드 설명은 생략한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
from typing import List, Optional
import numpy as np
from langchain.embeddings import OpenAIEmbeddings
from langchain.schema.embeddings import Embeddings
from sklearn.metrics import precision_score, recall_score, f1_score
from sklearn.metrics import roc_curve
from sklearn.mixture import GaussianMixture
def _normalize_vectors(vectors):
return vectors / np.linalg.norm(vectors, axis=1, keepdims=True)
class RedeSearchDetector:
"""
This class is implementation of REDE, the method for detect knowledge-seeking turn in few-shot setting.
It contains train function for your custom model, and inference function for detect knowledge-seeking turn.
You will need non-knowledge seeking turn dialogues. Plus, it will be great you have few knowledge-seeking turn dialogues.
The method is implementation of below paper:
@article{jin2021towards,
title={Towards zero and few-shot knowledge-seeking turn detection in task-orientated dialogue systems},
author={Jin, Di and Gao, Shuyang and Kim, Seokhwan and Liu, Yang and Hakkani-Tur, Dilek},
journal={arXiv preprint arXiv:2109.08820},
year={2021}
}
"""
def __init__(self,
threshold: float,
embedding: Embeddings = OpenAIEmbeddings()):
"""
:param embedding: Encoder model for encoding sentences to vectors. Langchain Embeddings class. Default is OpenAIEmbeddings.
:param threshold: Threshold for classify knowledge-seeking turn. If the score is higher than threshold, classify as non-knowledge-seeking turn.
Find this threshold by using training data that you own. (e.g. 0.5)
"""
self.embedding = embedding # Encoder model for encoding sentences to vectors
self.threshold = threshold
self.mu = None
self.omega_matrix = None # Omega matrix for linear transformation.
self.gmm = None # Gaussian Mixture Model for classify knowledge-seeking turn.
self.norm = None # Norm for normalize to unit vector.
def find_representation_transform(self,
knowledge_seeking_sentences: List[str],
L: Optional[int] = None,
):
"""
:param knowledge_seeking_sentences: Knowledge-seeking turn sentences. List[str].
:param L: Number of dimensions of the transformed representation. If None, use whole dimension.
Default is None.
"""
# find mu
vectors = np.array(self.embedding.embed_documents(knowledge_seeking_sentences))
self.mu = np.mean(vectors, axis=0)
# get covariance matrix
sigma = np.cov(vectors.T)
# singular value decomposition
U, S, V = np.linalg.svd(sigma)
# find omega matrix
self.omega_matrix = U @ np.sqrt(np.linalg.inv(np.diag(S)))
if L is not None:
self.omega_matrix = self.omega_matrix[:, :L]
print("REDE representation transform done.")
def representation_formation(self, vectors: np.ndarray) -> np.ndarray:
"""
:param vectors: Vectors after encoding. np.ndarray.
:return: Transformed vectors. np.ndarray.
"""
return (vectors - self.mu) @ self.omega_matrix
def train_density_estimation(self,
gmm: GaussianMixture,
non_knowledge_seeking_sentences: List[str]):
"""
:param gmm: Gaussian Mixture Model for classify knowledge-seeking turn. GaussianMixture. n_components must be 1.
:param non_knowledge_seeking_sentences: Non-knowledge-seeking turn sentences. List[str].
"""
self.gmm = gmm
sentence_vectors = np.array(self.embedding.embed_documents(non_knowledge_seeking_sentences))
transformed_vectors = np.array(
[self.representation_formation(sentence_vector) for sentence_vector in sentence_vectors])
# normalize to unit vector
transformed_vectors = _normalize_vectors(transformed_vectors)
self.gmm.fit(transformed_vectors)
def find_threshold(self,
valid_knowledge_seeking_sentences: List[str],
valid_non_knowledge_seeking_sentences: List[str]):
"""
Find threshold using Youden's index from validation data predictions.
:param valid_knowledge_seeking_sentences: knowledge-seeking turn sentences for validation. List[str].
You can put same sentences that you used for find_representation_transform function.
:param valid_non_knowledge_seeking_sentences: non-knowledge-seeking turn sentences for validation. List[str].
"""
true_scores = self._get_density_score(valid_knowledge_seeking_sentences)
false_scores = self._get_density_score(valid_non_knowledge_seeking_sentences)
y_true = np.concatenate([np.ones_like(true_scores), np.zeros_like(false_scores)])
y_score = true_scores + false_scores
fpr, tpr, thresholds = roc_curve(y_true, y_score)
idx = np.argmax(fpr - tpr)
self.threshold = thresholds[idx]
precision, recall, f1 = self._calculate_metrics(y_true, y_score)
print(f"Precision: {precision}")
print(f"Recall: {recall}")
print(f"F1: {f1}")
return self.threshold
def detect(self, sentences: List[str]) -> bool:
"""
:param sentences: Sentences to detect. List[str].
:return: True if the sentence is knowledge-seeking turn, else False. bool.
"""
score = self._get_density_score(sentences)[0]
return score < self.threshold
def evaluate(self, test_knowledge_seeking_sentences: List[str],
test_non_knowledge_seeking_sentences: List[str]):
"""
Evaluate rede search detector using test dataset.
:param test_knowledge_seeking_sentences: knowledge-seeking turn sentences for test. List[str].
:param test_non_knowledge_seeking_sentences: non-knowledge-seeking turn sentences for test. List[str].
"""
true_scores = self._get_density_score(test_knowledge_seeking_sentences)
false_scores = self._get_density_score(test_non_knowledge_seeking_sentences)
y_true = np.concatenate([np.ones_like(true_scores), np.zeros_like(false_scores)])
y_score = true_scores + false_scores
precision, recall, f1 = self._calculate_metrics(y_true, y_score)
print(f"Precision: {precision}")
print(f"Recall: {recall}")
print(f"F1: {f1}")
return precision, recall, f1
def _get_density_score(self, sentences: List[str]) -> List[float]:
sentence_vectors = np.array(self.embedding.embed_documents(sentences))
transformed_vectors = np.array([self.representation_formation(np.array(v)) for v in sentence_vectors])
transformed_vectors = _normalize_vectors(transformed_vectors)
scores = self._score_vectors(transformed_vectors)
return scores
def _score_vectors(self, vectors):
return [self.gmm.score(vector.reshape(1, -1)) for vector in vectors]
def _calculate_metrics(self, y_true, y_score):
predictions = np.where(y_score < self.threshold, 1, 0)
precision = precision_score(y_true, predictions)
recall = recall_score(y_true, predictions)
f1 = f1_score(y_true, predictions)
return precision, recall, f1